بازخوانی مطالعات دیوید رومر از مدلهای رشد اقتصادی (قسمت سوم)
بنای اقتصاد کلان بر پایه اقتصاد خرد

در نتیجه، برای اقتصاددانان تردیدی نمانده بود که باید اصلاحیهای بر این مدل اعمال شود تا بتوانند پدیده رشد اقتصادی و علت اختلاف درآمد سرانه میان کشورها را با دقت بالایی توضیح دهند و مهمتر از همه، پیشبینیهای دقیقتری در خصوص رشد اقتصادی انجام دهند. یکی از این اصلاحیهها مربوط میشود به مدل رشد اقتصادی که رومر در کتاب خود از آن با عنوان «مدل افق نامحدود» نام میبرد. آنها برای بنا کردن مدل خود، رهیافتهای نظریه اقتصاد خرد را مبنا قرار دادند. بنابراین، در این مدل علاوه بر رفتار بنگاه که در مدل سولو تمرکز اصلی بر آن بود، به رفتار خانوار نیز توجه میشود. در نتیجه این امر، در مدل افق نامحدود، نرخ پسانداز از یک نرخ ثابت و برونزا به یک نرخ متغیر و درونزا بدل میشود. بنابر فروض این مدل، خانوارها عمر نامحدودی دارند و درست از این جهت است که مدل، «افق نامحدود» نام گرفتهاست. مدل افق نامحدود نیز جز مدلهای نئوکلاسیک محسوب میشود که ابتدا توسط فرانک رمزی ایجاد شد و سپس، توسط دیوید کاس و تجلینگ کوپمنز گسترش پیدا کرد. از این نظر، ما در طول یادداشت، این مدل را با عنوان مدل رمزی-کاس-کوپمنز یاد خواهیمکرد. ضمنا ما در این یادداشت تنها فروض این مدل را شرح خواهیم داد و در یادداشت بعدی به نتایج حاصل از این فروض میپردازیم. همچنین، منبع اصلی این یادداشت نیز به مانند دو یادداشت سابق، ویرایش چهارم کتاب اقتصاد کلان پیشرفته دیوید رومر است که توسط منصور خلیل عراقی و علی سوری ترجمه شده و توسط انتشارات نور علم چاپ شدهاست.
مدل رمزی-کاس-کوپمنز به نوعی تجدیدنظر در مدل سولو محسوب میشود. این مدل در خصوص رشد اقتصادی که در حوزه نظریه اقتصاد کلان قرار میگیرد؛ بر پایه رهیافتهای نظریه اقتصاد خرد بنا شده است. در این مدل نرخ رشد نیروی کار (L) و نرخ رشد تکنولوژی (A) ثابت و برونزا در نظر گرفته میشود؛ اما، تغییرات موجودی سرمایه از رفتار حداکثرسازی خانوارها و بنگاهها استخراج میشود. در نتیجه، نرخ پسانداز در این مدل نه نرخی ثابت و برونزا که نرخی متغیر و درونزاست.
مدل رمزی-کاس-کوپمنز مدلی به نسبت ساده است. در این مدل، بنگاههای رقابتی، سرمایه را اجاره کرده و نیروی کار را استخدام میکنند تا درنهایت محصول خود را تولید کرده و بفروشند. مضاف بر این، تعدادی خانوار با عمر نامحدود وجود دارند که عرضهکننده نیروی کار هستند و این خانوارها درآمد خود را مصرف و پسانداز میکنند. لکن، نکته اساسی در فروض این مدل همان عمر نامحدود خانوارهاست که همین امر، منشأ ظهور و بروز مدل دایموند شد.
فروض مدل
در این مدل ما با دو بخش بنگاه و خانوار مواجه هستیم. پیرو رهیافتهای اقتصاد خرد نیز میدانیم که هر کدام از این بخشها به دنبال پیگیری اهداف خود یعنی حداکثرسازی مطلوبیت خویش هستند. در این راستا، بنگاهها رفتار مشابه بنگاهها در مدل سولو را دارند. در نتیجه، تابع تولید هر بنگاه مانند مدل سولو به شکل زیر است:
Y (t) = F (K (t) , A (t) L (t))
که Y مقدار محصول، K موجودی سرمایه، AL نیز نیروی کار موثر است که A همان موجودی دانش یا سطح بهرهوری و L همان تعداد نیروی کار است. بنا به آموزههای اقتصاد خرد نیز میدانیم که هر بنگاهی به دنبال حداکثرسازی سود خود است. این بنگاهها با کسب سرمایه و نیروی کار از بازارهای رقابتی، محصولات خود را تولید میکنند و از آنجا که این بنگاهها تحت مالکیت خانوارها قرار دارند، سود حاصل از کار تولید این بنگاهها به خانوارها تعلق میگیرد. مضاف بر این، باید توجه داشت که A برونزاست و مانند مدل سولو، نرخ رشد آن برابر با مقدار ثابت g است.
پس از بنگاه و فروض مربوطه به آن در این مدل، به خانوارها میرسیم. اندازه هر خانوار با نرخ ثابت و برونزای n رشد میکند. هر عضو خانوار، یک واحد نیروی کار در هر لحظه از زمان عرضه میکند و تعداد خانوارها با مقدار ثابت H برابر است. همچنین، در این مدل، جمعیت کل برابر (L (t است و در نتیجه، بعد خانوار در هر لحظه از زمان برابر با L (t) / H است. علاوه بر این، موجودی اولیه سرمایه برابر با (K (۰ است و در نتیجه، سهم هر خانوار از موجودی اولیه سرمایه برابر با K (۰) / H است. بدین معنا که در این مدل استهلاک سرمایه برابر با صفر است. هر خانوار، درآمد خود را که حاصل کار و سرمایه است؛ میان مصرف و پسانداز تقسیم میکند و این تقسیم به نحوی صورت میگیرد که مطلوبیت خانوار در طول عمر خود حداکثر شود. در نتیجه، مطلوبیت هر خانوار در هر لحظه را میتوان با رابطه زیر توضیح داد:
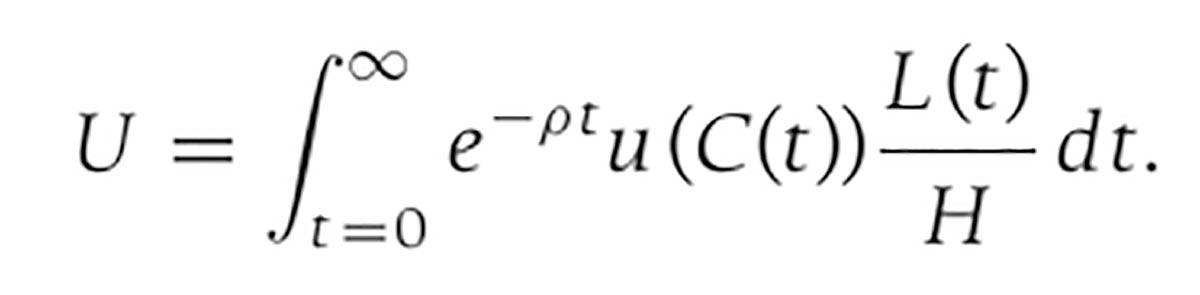
در این رابطه u (C (t)) همان مطلوبیت هر فرد در زمان t است و بنابراین، u (C (t)) . L (t) / H بیانگر مطلوبیت خانوار در زمان t است. در واقع، بنا به ادبیات نظریه اقتصاد خرد میدانیم که هدف هر فردی افزایش مطلوبیت است و مطلوبیت بیشتر از مصرف بیشتر حاصل میشود. همچنین، ρ نرخ تنزیل است که هر چقدر بزرگتر باشد، نشان میدهد که مصرفکننده، مصرف در زمان حال را به مصرف در آینده ترجیح میدهد. به عبارت دیگر، بزرگ بودن نرخ تنزیل حکایت از آن دارد که مصرفکننده صبور نیست و دوست دارد هر چه زودتر درآمد خود را مصرف کند.
علاوه بر این فروض مطرح شده در خصوص خانوارها، باید بیان داشت که فرض بعدی از این قرار است که تابع مطلوبیت در زمان t به این صورت است:
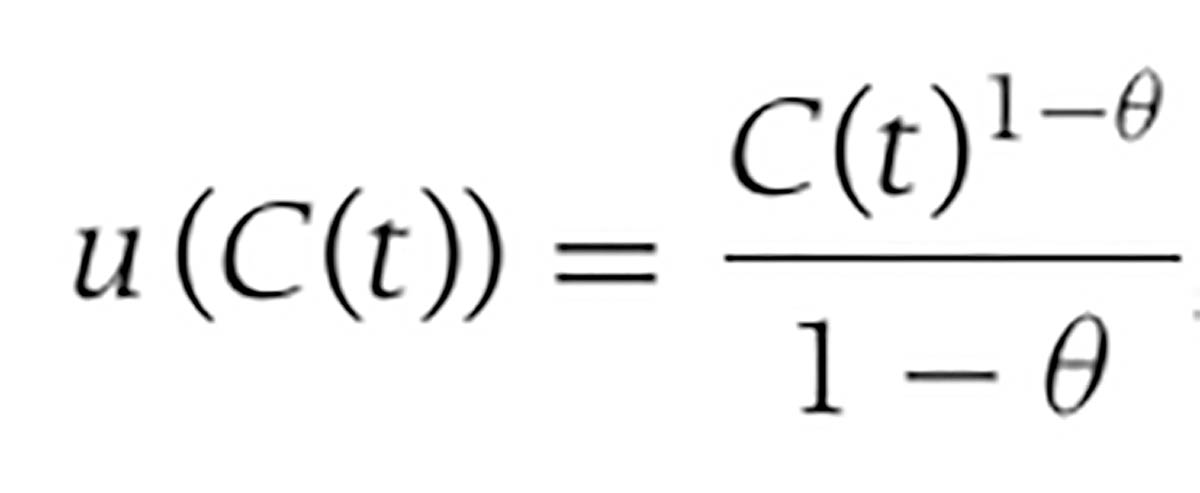
از این رابطه نیز این نتیجه حاصل میشود که مطلوبیت نهایی هر فرد از رابطه u’ (C) =1/ C θ حاصل میشود. پیرو این رابطه بدیهی است که هر چه اندازه θ بزرگتر باشد، مطلوبیت نهایی با سرعت بیشتری به صفر نزدیک میشود. حال با استنتاج رابطه مطلوبیت نهایی، شاخص ریسکگریزی مطلق یا همان ARA و شاخصی ریسکگریزی نسبی یا همان RRA را نیز میتوان استخراج کرد. این دو شاخص به ترتیب برابر میشوند با θ/ C و θ که نشان میدهند با افزایش مصرف، ریسکگریزی مطلق کاهش یافته؛ اما، ریسکگریزی نسبی همواره ثابت است و ربطی به میزان مصرف ندارد. در نتیجه، فرقی ندارد که شما شخص پردرآمدی باشید یا کمدرآمد، میزان ریسکگریزی نسبی شما با همدیگر برابر خواهد بود؛ اما، اگر پردرآمد باشید، با افزایش مصرف میتوانید ریسکگریزی مطلق خود را کاهش دهید. در رابطه با θ باید تصریح کرد که بیانگر تمایل خانوار به « انتقال مصرف از یک دوره به دوره دیگر » است. از این نظر است که هر چه θ بزرگتر باشد، مطلوبیت نهایی خیلی سریع به صفر میرسد. به بیانی دیگر، با افزایش اندکی در مصرف، مطلوبیت نهایی به صفر میرسد و مصرفکننده تمایل چندانی به تغییر در مصرف ندارد. برعکس این شرایط، هر چه θ کوچکتر باشد، مطلوبیت نهایی به آرامی کاهش پیدا میکند و در نتیجه، دامنه تغییرات مصرف میتواند بزرگتر باشد. به عنوان مثال، اگر θ=0 باشد، تابع مطلوبیت شکل خطی به خود میگیرد و از آنجا که مشتق اول یک تابع خطی عددی ثابت است؛ مقدار مطلوبیت نهایی فرد نیز به طور کلی برابر با مقدار ثابتی خواهد بود. در این شرایط، اگر میزان نرخ بهره تغییر کند، مصرفکننده با افزایش یا کاهش میزان مصرف زمان حال خود، به تغییر نرخ بهره پاسخ میدهد که در واقع از این طریق در حال تغییر میزان پسانداز خود است. بهطور کلی باید بیان داشت که θ به ما کمک میکند تا به تخمینی درباره میزان جانشینی بین زمانی مصرف برسیم. محاسبات ریاضی برآمده از فروض رمزی-کاس-کوپمنز به ما نشان میدهد که کشش جانشینی بین زمانی برابر با یک تقسیم بر θ است.
نتیجه
با باز شدن پای خانوارها به مدلهای رشد اقتصادی، فروض این مدلها نیز تغییر پیدا کرد. در واقع بین بنگاه مدل رمزی-کاس-کوپمنز و بنگاه مدل سولو تفاوتی وجود ندارد؛ اما، اضافه شدن طرف خانوار به مدل، تفاوت اساسی میان این دو مدل ایجاد میکند که نمود اصلی آن درونزا شدن و متغیر شدن نرخ پسانداز است. این نرخ از دل فروض مطرح شده در این یادداشت و رفتار خانوار قرار است محاسبه شود که در یادداشت بعدی به آن خواهیم پرداخت. لکن، تا همینجا متوجه شدیم که هدف خانوارها آن است که مصرف خود را در طول عمر خود حداکثر کنند. به این جهت، پای نرخ تنزیل به مدل باز میشود و خانوار بر این اساس تصمیم میگیرد که مصرف خود را بین زمان حال و آینده به نوعی توزیع کند که حداکثر مطلوبیت را در طول عمر خود به دست آورد.
نتیجه این توزیع بین دو دوره حال و آینده موجب تغییر میزان پساندازها میشود. با این توصیف، هدف ما در یادداشت بعدی، توضیح این مساله که این تفاوت میان مدل رمزی-کاس-کوپمنز و مدل سولو به چه نتایج متفاوتی ختم خواهد شد. لکن، تفاوت این دو مدل تنها به این سطح محدود نخواهدشد و مدل رمزی-کاس-کوپمنز، علاوه بر خانوار، پای دولت را نیز به مدل رشد اقتصادی باز خواهدکرد.















