«عجله دارم» از زاویه نظریه بازیها

فرض کنید یک مسافر (شروعکننده بازی) با توجه به ارزش زمان در رسیدن به مقصد خود و بودجه مدنظر بین سفر عادی و سفر گرانتر (عجله دارم)، سفر عادی را انتخاب کرده و دو راننده این درخواست سفر را میبینند. راننده اول که تاکنون در طول روز به حد کافی درآمد کسب نکرده یا به فرض در حال رفتن به محل کارش است و باید این مسیر ۳۰دقیقهای تا محل کار را سر موعد طی کند و راننده دومی به حد کافی از نظر ذهنی درآمد کسب کرده یا این سفر عادی برایش سرراست نیست و از نظر ذهنی برایش سفر پرهزینهای است. راننده اول زمان برایش کمتر از راننده دوم ارزش دارد و از قدرت چانهزنی کمتری برخوردار است. بنابراین پیشنهاد سفر برای او عقلانی است و از بیم ازدستدادن این سفر توسط سایر رانندهها پیشنهاد را قبول خواهد کرد و هر دو طرف سود اقتصادی خواهند برد. راننده دوم چون قدرت چانهزنی بالاتری دارد صبر میکند تا سفری با قیمت مناسبتری نصیبش شود. همانطور که مشاهده میشود، در این مورد رانندههایی همچون راننده دوم از میدان رقابت برای کسب چنین سفرهایی خارج میشوند (یا کناره میگیرند) و این سفرها بیشتر نصیب رانندههایی از نوع اول میشود.
![]()
![]()
در نتیجه با وجود گزینه «عجله دارم» افراد میتوانند از قدرت چانهزنی استفاده کنند و معاملات بهینهتری ایجاد شود. درواقع افراد با محاسبه ارزش زمانی خود مازاد مبادله (اختلاف قیمتی ذهنی و واقعی) را بهینهتر بین خود تقسیم میکنند و مسافر و راننده با ارزش زمانی برابر همدیگر را پیدا خواهند کرد.
مساله بعدی این فرض است که رانندههایی که حتی اگر از نظر ارزش زمانی با مسافر برابر باشند، سفر را قبول نمیکنند تا مسافر را مجبور به فعال کردن گزینه «عجله دارم» کنند. این فرض غلط است. اگر راننده درخواستی را ببیند و این درخواست برایش معقول باشد؛ اما با فرض احتمال اینکه با اندکی صبر (حداقل هزینه زمانی) مسافر را به فعالکردن گزینه «عجله دارم » ترغیب کند، صبر میکند. اما چون قیمت فعلی برای مسافر معقول است و زمان برای هر دو نفر ارزش یکسان دارد، مسافر نیز صبر میکند و در نتیجه راننده با رفتار عقلانی متوالی سفر را قبول میکند؛ چون صبر بیشتر از صبر مسافر ارزش آن را برای راننده با یک ضریبی میکاهد.
فرمول ارزش مقداری با درنظرگرفتن ارزش زمان:
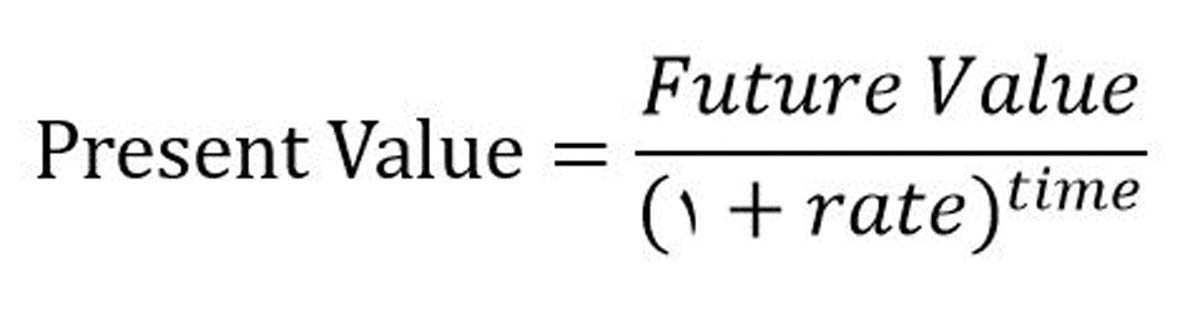
با فرض ارزش زمان برابر برای هر دو (مثلا نرخ 0.03 برای هر دو) حالات را به ترتیب مطلوبیت راننده امتیازبندی میکنیم:
اگر مسافر گزینه «عجله دارم» را از اول یا با صبر اندک فعال کند = 2
اگر سفر را در حالت عادی فعال کند =1
با صبر یکمرحلهای سفر عادی را قبول کند = 0.97 (۱(0.03+1) /1)
با صبر دومرحلهای منتظر مسافر بعدی است و احتمال 80درصد می دهد که مسافر بعدی وجود دارد که چنین سفری را با حالت «عجله دارم» درخواست کند = 0.82 ((۲(0.03+1)/2)0.8)
مطلوبیتهای مسافر:
سفر در حالت عادی قبول شود = 2
سفر با صبر یکمرحلهای قبول شود = 1.94(۱(0.03+1) /2)
سفر در حالت عجله دارم قبول شود = 1
با صبر دومرحلهای منتظر راننده بعدی است و احتمال 80درصد میدهد که راننده بعدی وجود دارد که چنین سفری را با حالت عادی قبول کند = 0.82 ((۲(0.03+1)/2)0.8)
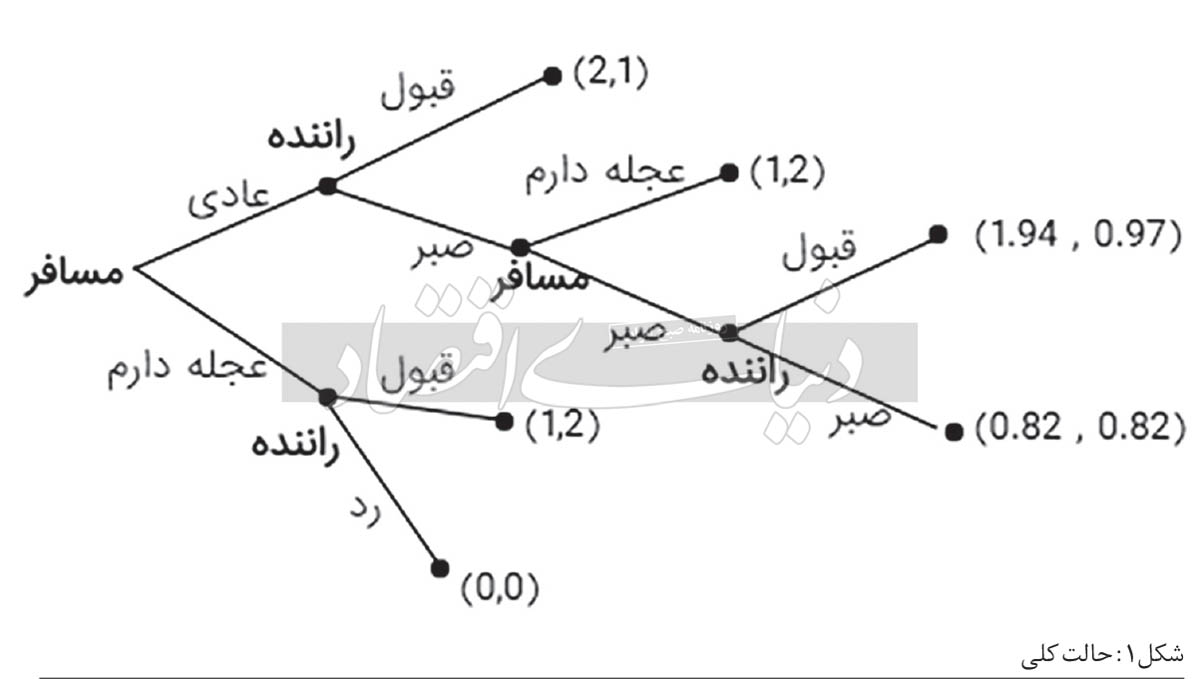
حالت بازی (شکل1):
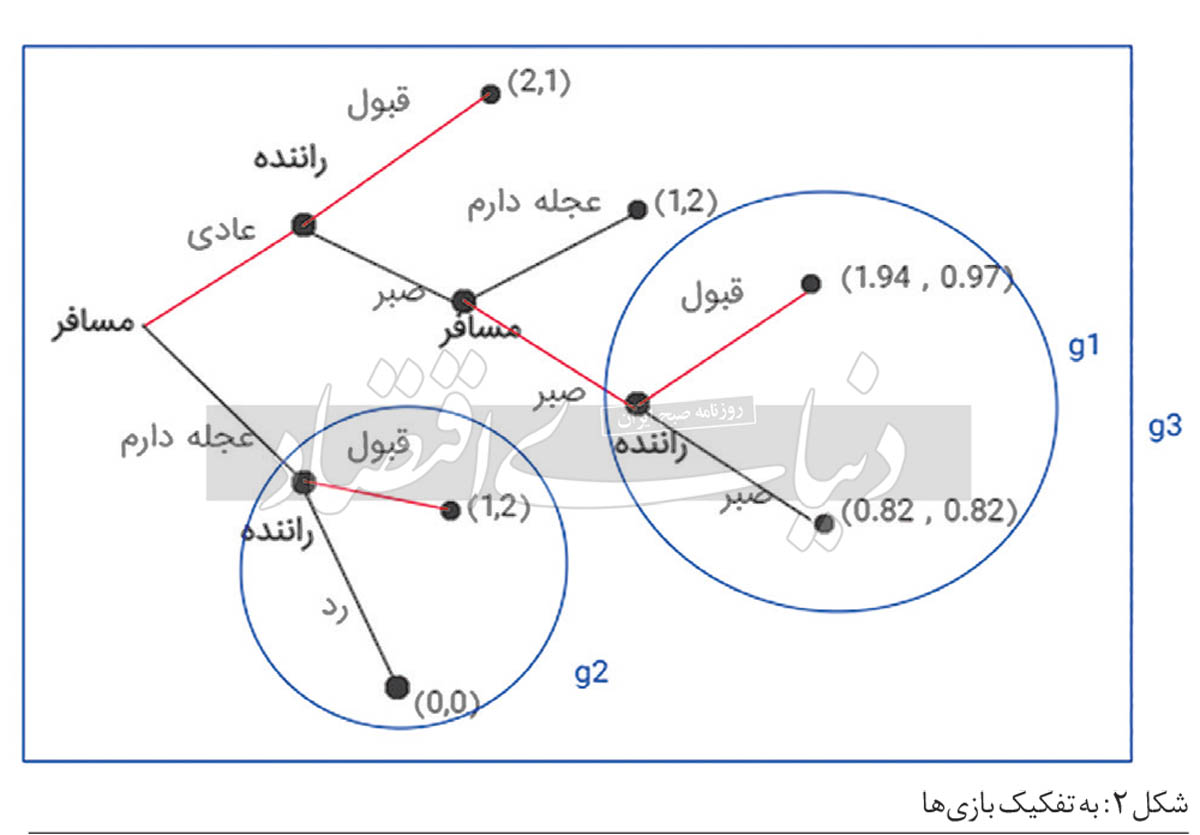
حال با حل بازگشت به عقب (backward induction) متوجه میشویم که در این حالت راننده سفر را در حالت عادی قبول میکند. راننده با نگاه به مرحله آخر بازی (g1) - شکل2 - متوجه میشود که بین قبول (0.97) و صبر(0.82)، قبول گزینه بهتری است. مسافر نیز بین عجله دارم (1) و صبر(1.92)، صبر را انتخاب می کند. از طرفی راننده در بازی g2 (زمانی که مسافر در مرحله اول «عجله دارم» را فعال می کند) طبیعتا بین قبول (1) یا رد(0)، قبول را انتخاب میکند. در نتیجه مسافر به طور کلی بین گزینه قبول در حالت عادی و قبول در حالت «عجله دارم»، قبول در حالت عادی را انتخاب میکند و بازی در اینجا به تعادل میرسد. پس دو گروه با تمایلات برابر ارتباط دوسر بردی را باهم برقرار میکنند و هیچیک به خاطر شرایط رقابتی تمایلی به خدعه نخواهد داشت و با دخالت دادن احساساتی مانند طمع، سایر رقبا جای آن را در بازار خواهند گرفت.
اما با حذف گزینه «عجله دارم» قدرت چانهزنی از بین میرود و مساله قیمتگذاری از طرف پلتفرمهای تاکسی اینترنتی میتواند معاملات را غیربهینه کند. اگر نگرانی ارگان مربوطه از وجود گزینه «عجله دارم» این است که رانندهها همگی بهعمد سفرهای عادی را قبول نمیکنند تا مسافر مجبور به فعالکردن گزینه «عجله دارم» شود، رفع این نگرانی با حذف این گزینه درست نیست؛ زیرا طرف عرضه (رانندهها) یک بازار رقابتی است و رفتهرفته تعداد رانندهها در حال افزایش است که باعث میشود عمل تبانی غیرممکن شود. از طرفی شاید در بعضی از مناطق شهری شاهد این عمل غیراخلاقی باشیم که علتش کمبودن راننده و افزایش قدرت تبانی است که در این صورت باید برای افزایش طرف عرضه سیاستی اتخاذ کرد و نه حذف این گزینه.















