دایره‌المعارف اقتصاد

معمای زندانی

آویناش ویکسیت و بری نیلبوف
مترجمان: محمدصادق الحسینی، محسن رنجبر
معمای زندانی (Prisoner’s Dilemma) شناخته‌شده‌ترین بازی استراتژیک در علوم اجتماعی است. این بازی به ما کمک می‌کند تا آنچه بر تعادل میان همکاری و رقابت در کسب‌وکار، سیاست و چینش‌های اجتماعی اثر می‌گذارد را درک نماییم.

آویناش ویکسیت و بری نیلبوف
مترجمان: محمدصادق الحسینی، محسن رنجبر
معمای زندانی (Prisoner's Dilemma) شناخته‌شده‌ترین بازی استراتژیک در علوم اجتماعی است. این بازی به ما کمک می‌کند تا آنچه بر تعادل میان همکاری و رقابت در کسب‌وکار، سیاست و چینش‌های اجتماعی اثر می‌گذارد را درک نماییم.

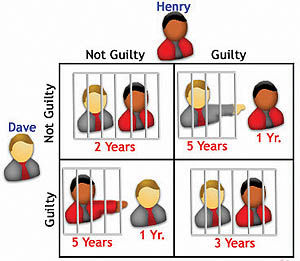
در گونه رایج این بازی چنین گفته می‌شود که پلیس دو مظنون را دستگیر کرده و در حال بازجویی از آنها در دو اتاق جداگانه است. هریک از این دو نفر می‌توانند اعتراف کنند و از این طریق پای فرد دیگر را هم به میان بکشند یا می‌توانند سکوت نمایند. در واقع فارغ از آنچه مظنون دیگر انجام می‌دهد هریک از این دو نفر می‌تواند با اعتراف کردن، موقعیت خود را بهبود ببخشد. در صورتی که یکی از این افراد اعتراف کند، آن‌گاه برای دیگری بهتر است که همین کار را انجام دهد تا از مجازات بسیار سختی که در انتظار مقاومت تمردآمیز است اجتناب ورزد. از طرف دیگر در صورتی که یکی از این مظنون‌ها ساکت بماند و دیگری اعتراف کند فرد اعتراف کننده می‌تواند انتظار داشته باشد که با او مانند یک شاهد (و نه یک مجرم) رفتار شود. از این رو اعتراف، استراتژی غالب (dominant strategy) (برای هریک از دو فرد مزبور خواهد بود(رجوع کنید به تئوری بازی‌ها). اما وقتی هر دوی آنها اعتراف می‌کنند، نتیجه‌ای که حاصل می‌شود بدتر از پیامد مربوط به زمانی خواهد بود که هر دو سکوت نمایند. مفهوم معمای زندانی توسط دو تن از دانشمندان شرکت رند (RAND) با نام‌های مریل فلاد و ملوین درشر شکل گرفت و توسط آلبرت تاکر، ریاضیدان دانشگاه پرینستون رسمیت یافت.
معمای زندانی دلالت‌ها و معانی ضمنی خاصی را در اقتصاد و بازرگانی دارد. دو شرکت مثل کوکاکولا و پپسی را در نظر بگیرید که محصولات مشابهی را به فروش می‌رسانند. هریک از این دو شرکت باید تصمیمی را در رابطه با استراتژی قیمت‌گذاری خود اتخاذ نمایند. زمانی این شرکت‌ها بهترین بهره را از قدرت مشترک خود در بازار خواهند برد که هر دوی آنها قیمت بالایی را به محصولات خود اعمال کنند. در این حالت هریک از آنها سودی مثلا به میزان ده میلیون دلار در ماه کسب خواهند کرد. اما اگر یکی از این دو شرکت قیمت پایینی را برای محصولاتش وضع نماید، تعداد بسیار زیادی از مشتریان شرکت دیگر را به سمت خود جذب خواهد کرد. فرض کنید سود این شرکت با این کار به دوازده میلیون دلار در ماه برسد و سود رقیب او به هفت میلیون دلار در ماه کاهش پیدا کند. اما در صورتی که هردوی آنها قیمت پایین را از مشتریان مطالبه نمایند، سود ماهانه هرکدام از آنها نه میلیون دلار در ماه خواهد بود. در این مثال استراتژی قیمت پایین مشابه اعتراف زندانی و قیمت بالا شبیه سکوت است. بیایید دو مورد اول (قیمت پایین و اعتراف زندانی) را تقلب و دو مورد آخر (قیمت بالا و سکوت) را همکاری بنامیم. پس تقلب، استراتژی غالب هریک از دو شرکت فوق است اما نتیجه حاصل برای هر یک از آنها زمانی که هر دو «تقلب می‌کنند» بدتر از حالتی است که هر دو به همکاری با یکدیگر می‌پردازند. مسابقات تسلیحاتی میان ابرقدرت‌ها یا کشورهای رقیب نیز نمونه مهم دیگری از این معما است. وقتی که هر دوی این قبیل کشورها به همکاری با یکدیگر پرداخته و از مسابقه تسلیحاتی دوری کنند، وضعیت هر دوی آنها بهتر خواهد بود. با این حال استراتژی غالب برای هریک از آنها این است که خود را به شدت مسلح نماید.
ظاهرا چنین به نظر می‌رسد که معمای زندانی با ایده دست نامرئی آدام اسمیت ناهم‌خوانی دارد. در معمای زندانی زمانی که هریک از دو طرف بازی به دنبال نفع شخصی خود است، نفع جمعی گروه را بهبود نمی‌بخشد. اما نکته مهم اینجاست که غالبا همکاری در یک گروه به نفع کل جامعه نیست. مثلا تبانی برای بالا نگه داشتن قیمت‌ها به نفع جامعه تمام نمی‌شود، چراکه معمولا هزینه این امر برای مشتری‌ها بیشتر از سود اضافی حاصل از آن برای شرکت‌ها است.
بنابراین شرکت‌هایی که با تقلب و سرپیچی از توافق‌نامه‌های تبانی‌آمیز به دنبال نفع خودشان هستند، در اغلب موارد به بقیه اعضای جامعه کمک می‌کنند. به همین نحو همکاری میان زندانی‌هایی که تحت بازجویی قرار دارند، باعث می‌شود که پلیس برای محکوم کردن آنها با مشکلات بیشتری مواجه شود. برای آنکه بتوان در پیگیری منافع عمده سیاستی به موفقیت رسید یا پیشرفت کرد، ابتدا باید مکانیسم همکاری را درک نمود.
آیا در حالتی که هریک از این «زندانی‌ها» انگیزه قوی و شدیدی برای تقلب دارند، دو طرف می‌توانند خود را از این تنگنا به در آورده و به همکاری خود ادامه دهند؟ اگر پاسخ مثبت است، چگونه می‌توانند این کار را انجام دهند؟ رایج‌ترین و معمول‌ترین مسیر برای همکاری از تکرار این بازی ناشی می‌شود. در مثال مربوط به دو شرکت پپسی و کوکاکولا تقلب در یک ماه باعث می‌شود که شرکتی که دست به تقلب زده است، دو میلیون دلار سود اضافی به دست آورد. اما تغییر موقعیت دو شرکت از همکاری متقابل به تقلب دوجانبه باعث می‌شود که یک میلیون دلار از بین برود. بنابراین اگر پس از تقلب در یک ماه شاهد اقدام متقابل طی دو ماه بعدی باشیم، نتیجه حاصل آن خواهد بود که سود اضافی ای که یک شرکت با تقلب به دست آورده بود از میان خواهد رفت.
هرگونه تنبیه و مجازات شدیدتری برای شرکتی که دست به تقلب بزند نیز مانعی آشکار در مقابل تقلب خواهد بود.
پنج نکته زیر ایده‌هایی که در بالا آمد را روشن‌تر می‌کند:
1 - پاداش حاصل از تقلب برای شرکت متقلب بلافاصله به دست می‌‌آید، در حالی که ضرر حاصل از مجازات در آینده به وجود خواهد آمد.
بنابراین در صورتی که نرخ تنزیل بازدهی‌ها و پاداش‌های آتی برای طرفین بازی بسیار زیاد باشد، ‌آنگاه ممکن است ضرر حاصل از تقلب آن‌قدر نباشد که برای ممانعت از تقلب کردن کفایت کند. از این رو امکان تداوم همکاری میان بازیکنان بسیار کم‌تحمل (مثل دولت‌ها) مشکل‌تر است.
2 - مجازات و تنبیه اثرگذار نخواهد بود، مگر آنکه بتوان تقلب را تشخیص داده و مجازات کرد. بنابراین زمانی که راحت‌تر بتوان فعالیت‌ها و اقدامات شرکت‌ها (مثل قیمت‌گذاری) را تشخیص داد، همکاری میان آنها بیشتر می‌شود و هرگاه این امر سخت‌تر باشد (مانند تصمیم‌گیری درباره ویژگی‌های غیرقیمتی کالاها از قبیل ضمانت تعمیر)، شرکت‌ها به میزان کمتری با یکدیگر همکاری خواهند کرد. معمولا شکل‌دهی و سامان‌دهی مجازات و تنبیه در گروه‌های بسته و کوچک‌تر راحت‌تر است. بنابراین احتمال تبانی در صنایعی که شرکت‌های محدودی در آنها وجود دارد و خطر ورود رقبای جدید به آنها کمتر است، بیشتر خواهد بود.
۳ - می‌توان با تبعیت از استراتژی‌هایی مثل «مقابله به مثل»، مجازات را اتوماتیک کرد. این ایده توسط رابرت آکسلراد، دانشمند علوم سیاسی دانشگاه میشیگان به زبانی ساده بیان شد و متداول گردید. مقابله به مثل به این معنا است که اگر و تنها اگر رقیب فرد در دور پیشین بازی تقلب کرده باشد، آن‌گاه او نیز دست به تقلب خواهد زد. اما در صورتی که امکان سوءبرداشت از اقدامات سالم و بی‌غرضانه رقبا به عنوان تقلب وجود داشته باشد، آنگاه اتخاذ استراتژی مقابله به مثل خطر بروز دورهای متوالی تلافی غیرضروری را به وجود خواهد آورد.
4 - تعداد ثابت و محدود تکرار بازی منطقا برای ایجاد همکاری کافی نیست. هر دو یا تمام طرفین بازی می‌دانند که استراتژی غالب در دور آخر بازی، تقلب است. با توجه به این نکته، همین امر در یک دور مانده به آخر، دو دور مانده به آخر و... نیز صادق خواهد بود. اما در صحنه عمل شاهد هستیم که در دورهای ابتدایی از مجموعه ثابتی از تکرار‌ها، مواردی از همکاری روی می‌دهد. دلیل این امر آن است که یا بازیکن‌ها تعداد دورها را به طور قطعی نمی‌دانند یا اینکه می‌توانند از احتمال «خوب بودن غیرعقلایی» (irrational niceness) در راستای منافع مشترک خود بهره گیرند.
۵ - همکاری همچنین می‌تواند در صورتی بروز پیدا کند که گروه رهبری داشته باشد که از آنجا که در صورت رقابت شدید به تنهایی خسارت زیادی را متحمل می‌شود، باز هم محدودیت‌هایی را اعمال نماید حتی با وجودی که می‌داند سایر بازیگران کوچک تقلب خواهند کرد.
نقش عربستان سعودی به عنوان «تعدیل‌کننده نوسان» (swing producer) در کارتل اوپک نمونه‌ای از این حالت است.

درباره نویسنده‌ها
آویناش دیکسیت استاد اقتصاد دانشگاه پرینستون و بری نیلباف استاد مدیریت در دانشکده مدیریت دانشگاه ییل است. آنها نویسندگان کتاب «تفکر به شیوه استراتژیک» هستند.

منابعی برای مطالعه بیشتر
Axelrod, Robert. The Evolution of Cooperation. New York: Basic Books, 1984.
Dixit, Avinash, and Barry Nalebuff. Thinking Strategically: A Competitive Edge in Business, Politics, and Everyday Life. New York: W. W. Norton, ۱۹۹۱.
Hofstader, Douglas. "Mathamagical Themas." Scientific American (May 1983): 16-26.
Poundstone, William. Prisoner's Dilemma: John von Neumann, Game Theory, and the Puzzle of the Bomb. New York: Doubleday, ۱۹۹۲.
Rapoport, Anatol, and A. M. Chammah. Prisoners' Dilemma. Ann Arbor: University of Michigan Press, 1965.
"Prisoner's Dilemma." Wikipedia, online at: http://en.wikipedia.org/wiki/Prisoner%۲۷s_dilemma.
Kreps, David, Robert Wilson, Paul Milgrom, and John Roberts. "Rational Cooperation in the Finitely Repeated Prisoners' Dilemma." Journal of Economic Theory 27, no. 2 (August 1982): 245-252.
Milgrom, Paul. "Axelrod's The Evolution of Cooperation." RAND Journal of Economics ۱۵, no. ۲ (۱۹۸۴): ۳۰۵-۳۰۹.