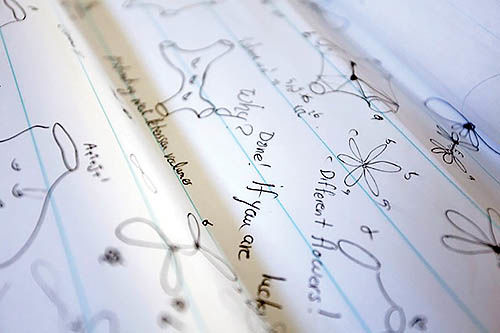پایان یک ذهن زیبا بخشی از محاسبات مریم میرزاخانی که پیش‌بینی می‌شود در آینده به گشایش‌های جدیدی در علم ریاضیات منتج شود

دنیای اقتصاد: پژوهشگران علوم ریاضی در توصیف کارهای علمی «مریم میرزاخانی» از تعبیر «چراغی که برخی از نقاط تاریک علم ریاضی را روشن کرد، استفاده کرده‌اند. مهم‌ترین بخش از پژوهش‌های این ریاضیدان برجسته در حوزه «هندسه هذلولی» متمرکز بوده‌ است. وی در پایان‌نامه مقطع دکترای خود برای نخستین بار به مساله‌ محاسبه تعداد خطوط راست بر سطح یک هذلولی پاسخ داد.

وی همچنین توانست ارتباطاتی برای دو پرسش اصلی پژوهشی دیگر ایجاد و هر دو را حل کند. اولی فرمولی برای محاسبه حجم فضای موسوم به «مدول» بود. او افزون بر این یک اثبات جدید و عجیب از یک حدس قدیمی مورد سنجش‌های توپولوژیکی خاص فضاهای مدولی مرتبط با نظریه ریسمان است که توسط «اوارد ویتن»، فیزیکدان موسسه تحقیقات پیشرفته در پرینستون ارائه شده بود، ارائه کرد. یافته‌های این دانشمند برجسته باعث شد تا مریم میرزاخانی در سال ۲۰۰۵ از سوی موسسه «پاپیولار‌ساینس» به‌عنوان ذهن برتر در حوزه ریاضیات معرفی شود. اگرچه حالت‌انتزاعی حجم دونات‌های نافرم بسیاری از دانشمندان را برای یافتن راه‌حلی برای محاسبه حجم این اشکال انتزاعی ناامید کرده بود، اما مریم میرزاخانی با ترسیم یک سری حلقه روی سطح این اشکال پیچیده به محاسبه حجم آنها پرداخت. پژوهش‌های علمی باعث شد تا اتحادیه جهانی ریاضیات، برای نخستین بار جایزه «فیلدز» را به یک زن اهدا کند. جایزه‌ای که از آن با عنوان «نوبل ریاضیات» نیز یاد می‌کنند. محاسباتی که می‌تواند در آینده باعث پاسخ به بسیاری از سوالات در رابطه با شکل و حجم جهان باشد. تحقیقات وی طیف گسترده‌ای از مباحث ریاضی را، از هندسه جبری و دیفرانسیلی تا فرآیندهای تصادفی، به‌هم پیوند داده است. زمینه‌ تحقیقاتی وی، دینامیک، در مقایسه با دیگر شاخه‌های مهم ریاضیات (همچون نظریه اعداد، هندسه مسطحه و آنالیز) موضوعی بسیار نوپاست.

مرگ بانوی نخستین‌ها

مریم میرزاخانی نخستین دختری بود که به تیم المپیاد ریاضی ایران راه یافت؛ نخستین دختری بود که در المپیاد ریاضی ایران طلا گرفت. او نخستین کسی بود که دو سال پیاپی در المپیاد جهانی ریاضی مدال طلا گرفت و نخستین فردی بود که در آزمون المپیاد ریاضی جهانی نمره کامل گرفت. مریم میرزاخانی پس از سپری کردن دورانی درخشان در دبیرستان برای تحصیل در رشته «ریاضیات» وارد دانشگاه «صنعتی شریف» شد. جایی که نگاه متفاوت او به حل مسائل ریاضی، بارها تحسین اساتید برجسته این دانشگاه را برانگیخت تا جایی که دکتر «آرش رستگار»، عضو هیات علمی دانشگاه صنعتی شریف، توانایی حل مساله این بانوی فقید ایرانی را بی‌بدیل توصیف می‌کند. میرزاخانی را می‌توان بازمانده یکی از طلایی‌ترین نسل‌های نخبگان ریاضی کشور دانست. نسلی که سقوط اتوبوس در حال بازگشت از «مسابقات ریاضی دانشجویی اهواز» در اسفند سال ۱۳۷۶، فرصت افتخارآفرینی بیشتر را از ۷ تن از آنها گرفت. میرزاخانی تحصیلات کارشناسی و کارشناسی ارشد خود را در رشته ریاضیات در دانشگاه صنعتی شریف به پایان رساند و در سال ۲۰۰۰ موفق به اخذ بورسیه تحصیلی در مقطع دکترا از دانشگاه «هاروارد» شد. استاد راهنمای مریم میرزاخانی در دانشگاه هاروارد «کورتیس مک‌مولن» یکی از برجسته‌ترین اساتید در رشته «توپولوژی» و برنده جایزه «فیلدز» در سال ۱۹۹۸ بود. به گفته این استاد برجسته ریاضیات، یکی از سمینارهای برگزار شده با موضوع «هندسه هذلولی» (هندسه لباچفسکی) مریم میرزاخانی را بیش از پیش مجذوب «حلقه‌های هذلولی» کرد. اشتیاقی که بر «بلندپروازی بی‌باکانه» این بانوی ریاضیدان افزود. مک‌مولن در توصیف مریم میرزاخانی از ذهن خلاقی صحبت می‌کند که می‌توانست از همان روزهای ابتدایی با تجسم صفحاتی که نمی‌توانستند در دنیای حقیقی وجود داشته ‌باشند، ذهن استاد راهنمای خود را با پازل‌های جذابی روبه‌رو می‌کرد. این سطوح دوناتی شکل دارای دو یا چند سوراخ هستند که از یک هندسه غیراستاندارد پیروی می‌کنند. هر نقطه از این سطح را می‌توان یک «نقطه زینی شکل» دانست. دونات‌های هذلولی را نمی‌توان در فضای عادی ساخت چرا که در حس انتزاعی وجود دارند و فواصل و زوایا بر اساس مجموعه خاصی از معادلات محاسبه می‌شوند. هر یک از این احجام تجسمی از بی‌نهایت حالت مختلف از ساختارهای هذلولی تشکیل می‌شوند و امروزه به‌عنوان یکی از مدرن‌ترین پل‌های ارتباطی بین علوم ریاضی و فیزیک شناخته ‌می‌شوند.

حیرت‌آفرینی با سطوح هذلولی

هنگامی که مریم میرزاخانی، تز دکترای خود را در دانشگاه هاروارد آغاز کرده‌بود، تعداد «ژئودزیک‌ها» یا خطوط راست در سطح هذلولی یکی از مسائل حل‌نشده علم ریاضیات بود. بر مبنای قوانین اثبات‌شده ریاضی برخی از این ژئودزیک‌ها دارای طول بی‌نهایت هستند، در حالی که برخی دیگر از این خطوط اصطلاحا راست در یک حلقه بسته کوچک قرار می‌گیرند. مریم میرزاخانی در پایان‌نامه دکترای خود توانست به این مساله پاسخ دهد. وی همچنین توانست ارتباطاتی برای دو پرسش اصلی پژوهشی دیگر ایجاد و هر دو را حل کند. اولی فرمولی برای محاسبه حجم فضای موسوم به «مدول» بود که به مجموعه‌ای از همه ساختارهای هذلولی ممکن در یک سطح ارائه شده گفته می‌شود. دومین موفقیت یک اثبات جدید و عجیب از یک حدس قدیمی است در مورد سنجش‌های توپولوژیکی خاص فضاهای مدولی مرتبط با نظریه ریسمان است که از سوی «اوارد ویتن»، فیزیکدان موسسه تحقیقات پیشرفته در پرینستون ارائه شده بود. این حدس به قدری مشکل بود که «ماکسیم کنتسویچ» از موسسه مطالعات پیشرفته علمی وجوی در پاریس به‌عنوان اولین ریاضیدانی که توانست آن را اثبات کند، در سال ۱۹۹۸ توانست مدال فیدلز را به‌صورت مشترک به‌دست آورد.

اولین‌ها برای دختر نابغه

میرزاخانی پس از فارغ‌التحصیلی از دانشگاه استنفورد، به‌عنوان استاد دانشکده ریاضی در دانشگاه «پرینستون» مشغول به تدریس شد. یک سال پس از فارغ‌التحصیلی در سال ۲۰۰۵، مجله «پاپیولار ساینس» مریم میرزاخانی را به‌عنوان یکی از ۱۰ متفکر خلاق جهان و ذهن برتر در رشته ریاضیات معرفی کرد. وی پس از سه سال تدریس در دانشگاه پرینستون، با عنوان استاد پژوهشگر به دانشگاه استنفورد رفت. در سال ۲۰۰۹ به خاطر دستاوردهایش در ریاضیات برنده جایزه «بلو منتال» شد. این جایزه هر چهار سال یک بار به کسانی که در رشته ریاضیات محض مشارکت قابل توجهی داشته‌اند اهدا می‌شود. در اعلامیه‌ای که انجمن ریاضی آمریکا به مناسبت برنده‌شدن این جایزه برای میرزاخانی منتشر کرد، دلیل گرفتن این جایزه معتبر « خلاقیت استثنایی او در یک پایان نامه مبتکرانه» عنوان شد. پایان نامه‌ای که به سه مورد از پیچیده‌ترین مسائل ریاضی پاسخ داده‌بود. میرزاخانی در سال ۲۰۱۰ نیز یکی دیگر از حدس‌های اثبات نشده علم ریاضیات به نام «شار‌زلزله» را برای نخستین بار در قالب اصول و قوانین ریاضی به اثبات رساند. وی در سال ۲۰۱۴ و پیش از دریافت جایزه جهانی «فیلدز» به همراه دو تن از دیگر پژوهشگران ریاضیات، فرضیه منظم بودن «ژئودزیک‌های مختلط و بستارهای آنها» را به اثبات رساند. اتحادیه جهانی ریاضی در یادداشتی با عنوان «کار مریم میرزاخانی» یافته‌های این پژوهشگر در زمینه یادشده را «شگفت‌آور» توصیف کرد. این نبوغ حیرت‌آور در کنار پشتکار بی بدیل این بانوی ایرانی، باعث شد که «اتحادیه جهانی ریاضیات» در سال ۲۰۱۴ برای نخستین بار جایزه فیلدز را به یک زن اهدا کند. این جایزه که از آن با عنوان جایزه «نوبل» در علم ریاضیات یاد می‌شود، به ریاضیدانانی اهدا می‌شود که در چهار دهه نخست زندگی خود توانسته باشند، کار ارزنده‌ای در علم ریاضیات انجام داده‌باشند. کمیته مدال فیلدز در توصیف مریم میرزاخانی از تعبیر «چیره‌دست در گستره‌ قابل توجهی از تکنیک‌ها و حوزه‌های متفاوت ریاضی، او تجسم ترکیبی کمیاب است از توانایی تکنیکی، بلندپروازی جسورانه، بینش وسیع و کنجکاوی ژرف» استفاده کرد. پیچیدگی موضوع مورد مطالعه این دانشمند برجسته ایرانی تا به حدی بود، که وی در نخستین گفت‌وگوی خود با یک رسانه‌ایرانی در پاسخ به سوال خبرنگار «دنیای‌اقتصاد» ارائه تصویر همه‌فهم از کارهای پژوهشی خود را بسیار دشوار دانسته بود. تحقیقات وی طیف گسترده‌ای از مباحث ریاضی را از هندسه جبری و دیفرانسیلی تا فرآیندهای تصادفی، به‌هم پیوند داده است. زمینه‌ تحقیقاتی وی، دینامیک، در مقایسه با دیگر شاخه‌های مهم ریاضیات (همچون نظریه اعداد، هندسه مسطحه و آنالیز) موضوعی بسیار نوپا است. دینامیک به بررسی هر سیستمی می‌پردازد که رفتارش در طول زمان بر اساس قانون مشخصی تغییر می‌کند. در یک مدل‌سازی ساده این سیستم به‌صورت یک میز بیلیارد با تعدادی توپ روی آن است. قانونی که بر حرکت این توپ‌ها حاکم است، این است که با شلیک هر توپ به هر جهتی، توپ در همان جهت به حرکت درمی‌آید و به حرکت خود با سرعت ثابت ادامه می‌دهد، مگر آنکه با توپ دیگری یا دیواره‌ها برخورد کند که در این صورت منعکس می‌شود. نه اصطکاک، نه چرخیدن توپ به دور خود و نه خیلی چیزهای دیگر در این تحلیل در نظر گرفته نمی‌شود. با این وجود تحلیل حرکت توپ‌ها پیچیدگی خاص خودش را دارد. ریاضیدانان به این مسائل می‌پردازند چون از این طریق به مدل‌سازی مسائل پیچیده‌تری، مثل حرکت مولکول‌های گاز در یک اتاق، دست پیدا می‌کنند. مثال فوق حالت بسیار ساده‌ای بود. در حقیقت تحلیل‌های دینامیکی بسیار پیچیده‌تر هستند و رفتار اجزای هر سیستمی تابع قوانین بسیار پیچیده‌تری هستند. میرزاخانی یکی از مهم‌ترین کارهای خود را بر اساس حرکت‌های ممکن یک توپ بیلیارد بر میز بیلیارد آغاز کرد. او با مهارتی عجیب دینامیک و هندسه را با یکدیگر تلفیق کرده و آن را به‌کار گرفت. البته قواعد بسیار پیچیده‌ای بر سیستم‌های مورد بررسی وی حاکم بود. قوانینی که بسیار به ریاضیات مدرن شبیه است و در مقایسه با قوانین مطرح شده، حالتی انتزاعی دارد. برای مثال، دینامیک‌هایى که او مطالعه مى‌کند، به‌طور مستقیم به حرکت توپ‌هاى بیلیارد روى میز نمی‌پردازد؛ بلکه به تغییرات میز بیلیارد که به شیوه‌اى منظم مشغول تغییر شکل است، می‌پردازد. در واقع، میز مانند یک سیاره عجیب در فضاى کهکشانی تمام میزهاى بیلیاردی که ممکن است وجود داشته باشند، می‌چرخد. مجموعه اقدامات وی در این زمینه باعث شد تا مریم میرزاخانی‌ در ادامه موفقیت‌های خود، در سال ۲۰۱۶ به‌عنوان نخستین دانشمند ایرانی به عضویت «آکادمی ملی علوم آمریکا» در آمد.

خاموشی جواهر در معادله تقدیر

اگرچه درهم‌تنیدگی نام مریم میرزاخانی با موفقیت‌های علمی، همواره دربردارنده اخبار شیرینی در ذهن مردم ایران و دوستداران علم ریاضیات بود، اما طی دو روز گذشته اخبار رسیده از این جواهر بی‌بدیل ریاضیات، حاوی خبرهای تلخی بود. در روز پایانی هفته گذشته و به دنبال وخامت حال مریم میرزاخانی، خبر ابتلای جواهر ایرانی به بیماری سرطان در فضای خبری منتشر شد. بر مبنای اخبار منتشر شده، مریم میرزاخانی از حدود ۴ سال پیش به بیماری سرطان سینه مبتلا بوده است. پیشروی این بیماری باعث سرایت سرطان به مغز استخوان وی و لاینحل شدن معادله بیماری او برای پزشکان شده بود. این بیماری در نهایت در صبحگاه روز گذشته باعث محروم شدن جهان ریاضیات از خلاقیت‌هایی شد که می‌توانست «جنگل نا‌آشنای ریاضیات انتزاعی را بیش از پیش برای محققان ریاضی روشن کند». وی در تلاش بود تا ابعاد گوناگون فرم‌های هندسی غیر طبیعی را حل کند. با فرض تبعیت جهان از قاعده هندسه هذلولی، ابتکار وی به ارائه تعریف دقیق از شکل و حجم جهان کمک خواهد کرد. اگرچه دشواری محاسبه حجم اشکال هذلولی به شکل دونات‌های نافرم بسیاری از ریاضیدانان را نا امید کرده بود، مریم میرزاخانی با ترسیم یکسری حلقه روی سطح این اشکال پیچیده به محاسبه حجم آنها پرداخت. محاسباتی که می‌تواند در آینده باعث پاسخ به بسیاری از سوالات در رابطه با شکل و حجم جهان باشد. میرزاخانی در توصیف نگاه خود به زندگی گفته‌بود: «باید میوه‌های شاخه‌های پایین را ندیده گرفت، نباید گذاشت که این میوه‌ها ما را فریب دهند و از شاخه‌های بالاتر غافلمان کنند. راستش من مطمئن نیستم این نگاهی که من دارم درست باشد، اما این را می‌دانم که من از این سبک زندگی لذت می‌برم و تصور می‌کنم که زندگی قرار نیست خیلی هم راحت باشد».

هجرت ابـدی ملکـه ریاضیـات

ریاضی به درست فکرکردن کمک می‌کند